Last Digit

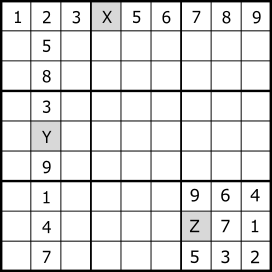
"Last Digit" is a rule of numerical arrangement of Sudoku.
In a house with one indeterminate cell, that cell is determined to the remaining digits.

For this example, set X=4 Y=6 Z=8.

Example

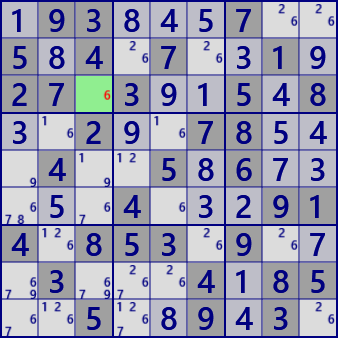
Cells with dark background are problem digits, light cells are solved cells, small digits are candidate digits

The r3c3 is determined to be digit 6.

.93...7..5.4.7..1.27.3..5.8..2..78...4..5.6.....4...914.853.9...3...4.85..5..9.3.

If simple program, it will be the following code.

Last Digit C# program(simple program)

partial class GNPZ_Analyzer{		
    public bool gSDK_LastDigitOld( ){
        int rc=0;
        UCell P0=null;
        
        for( int tfx=0; tfx<27; tfx++ ){
            int cc=0;
            for( int nx=0; nx<9; nx++ ){
                UCell P = GetCell_House( pBDL, tfx, nx, ref rc );
                if( P.No==0 ){
                    if( ++cc>=2 ) goto nextTry;
                    P0 = P;
                }
            }
            if( cc==1 ){
                SolCode=1;
                P0.FixedNo = P0.FreeB.BitToNum()+1;
                if( !MltSolOn )  goto LFond;
            }
        nextTry:
            continue;
        }

      LFond:
        .
        . (Solution report code)
        .
		return true;
    }
    private UCell GetCell_House( List<UCell> pBDL, int tfx, int nx, ref int rc ){ //nx=0...8
        int r=0, c=0, fx=tfx%9;
        switch(tfx/9){
            case 0: r=fx; c=nx; break;  //row
            case 1: r=nx; c=fx; break;  //column
            case 2: r=(fx/3)*3+nx/3; c=(fx%3)*3+nx%3; break; //block
        }
        return pBDL[r*9+c];
    }
}

Next is the Linq version. The essential part of the analysis algorithm is one line.
if( pBDL.IEGetCellInHouse(tfx,0x1FF).Count()==1 )
IEGetCellInHouse is defined as a static class with other similar functions as an extension function of List type.

Last Digit C# program(Linq version)

public class SimpleSingleGen: AnalyzerBaseV2{
    public bool LastDigit( ){
        bool  SolFond=false;
        for( int tfx=0; tfx<27; tfx++ ){
            if( pBDL.IEGetCellInHouse(tfx,0x1FF).Count()==1 ){
                SolFond=true;
                var P=pBDL.IEGetCellInHouse(tfx,0x1FF).First();
                P.FixedNo=P.FreeB.BitToNum()+1;                 
                if( !MltSolOn )  goto LFond;
            }
        }

        LFond:
        if(SolFond){
            .
            . (Solution report code)
            .
			return true;
        }
        return false;
    }
}

IEGet function

static public class StaticSA{ 
    static public IEnumerable<UCell> IEGetCellInHouse(this List<UCell> pBDL, int tfx, int FreeB=0x1FF){
        int r=0, c=0, tp=tfx/9, fx=tfx%9;
        for( int nx=0; nx<9; nx++ ){
            switch(tp){
                case 0: r=fx; c=nx; break;//row
                case 1: r=nx; c=fx; break;//column
                case 2: r=(fx/3)*3+nx/3; c=(fx%3)*3+nx%3; break;//block
            }
            UCell P=pBDL[r*9+c];
            P.nx=nx;
            if( (P.FreeB&FreeB)>0 ) yield return P;
        }
    }
}