LockedCandidate

LockedCandidate has two types.

Type 1

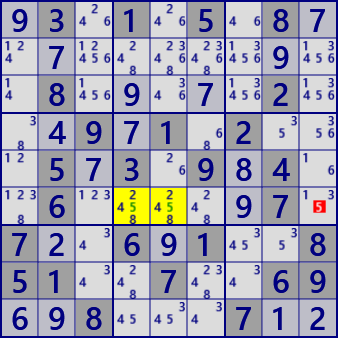
If the digit N is only one row in the block, it is excluded from the same row of the other block. This also applies to the column direction.

In block b5, the digit #5 is only r6.
Therefore, in r6c9 of block b6, the digit #5 is excluded from the candidates.

.3.1.5.8...........8.....2...9.1.2...5.3.9.4..6.....7.7..6.1..851..7..69..8...7..

type 2

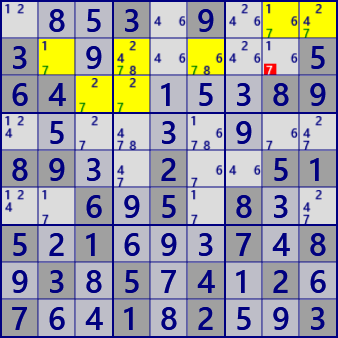
LockedCandidate type 2 is a solution that limits where the digits of the remaining blocks are located when there are digits in only two lines of two blocks.

Focus on the #7 in the figure on the left. In b1 and b2, #7 exists only in r1 and r2. At this time, in b3, #7 is in r1. Therefore, in b3, #7 is not in r2 and r3.

...3.9...3.......564.....89.........89..2..51..6.5.8..5.1...7.8.3.5.4.2.7..1.2..3

LockedCandidate C# program

The essential analysis part is about 10 steps in each of types 1 and 2.

public class LockedCandidateGen: AnalyzerBaseV2{
    public LockedCandidateGen( GNPX_AnalyzerMan pAnMan ): base(pAnMan){ }

    public bool LockedCandidate( ){
        for( int no=0; no<9; no++ ){
            int noB=(1<<no);
            int[] BRCs = new int[9];
            foreach( var P in pBDL.Where(Q=>(Q.FreeB&noB)>0) ){ BRCs[P.b] |= (1<<P.r)|(1<<(P.c+9)); }

            //==== Type-1 =====
            for( int b0=0; b0<9; b0++ ){
                for( int hs=0; hs<10; hs+=9 ){  //0:row 9:collumn
                    int RCH=BRCs[b0]&(0x1FF<<hs);
                    if( RCH.BitCount()==1 ){
                        int hs0=RCH.BitToNum(18);
                        if( pBDL.IEGetCellInHouse(hs0,noB).Any(Q=>Q.b!=b0) ){ //Type 1 is found
                           .
                           . (Solution report code)
                           .
                           return true;
                        }
                    }
                }
            }
            
            //==== Type-2 =====
            for( int b0=0; b0<9; b0++ ){
                int b1, b2, rcB0, rcB1, rcB2;
                for( int hs=0; hs<10; hs+=9 ){  //0:row 9:collumn
                    int hsX=0x1FF<<hs;
                    if(hs==0){b1=b0/3*3+(b0+1)%3;b2=b0/3*3+(b0+2)%3;}// b1,b2:block(row direction)
                    else{     b1=(b0+3)%9;       b2=(b0+6)%9;}   // b1,b2:block(collumn direction)

                    if( (rcB0=BRCs[b0]&hsX).BitCount() <=1 )  continue;
                    if( (rcB1=BRCs[b1]&hsX) <=0 )  continue;
                    if( (rcB2=BRCs[b2]&hsX) <=0 )  continue;

                    int rcB12 = rcB1|rcB2;
                    int hs0=(rcB0.DifSet(rcB12)).BitToNum(18);
                    if( rcB12.BitCount()==2 && hs0>=0 ){ //Type 2 is found
                       .
                       . (Solution report code)
                       .
                       return true;
                    }
                }
            }
        }
        return false;
    }
}