Locked

For Sudoku's advanced analysis algorithms, the concept "Locked" is important. Locked is a limitation on the cell(s) candidate diigits, the diigit of candidate digits, and the arrangement of cells, Candidate diigits are limited, or candidate diigits are excluded.
There are several types of Locked, and there are as many analysis algorithms as there are

Naked LockedSet

LockedSet is the simplest Locked analysis algorithm.
Focusing on n cells in a house, when these candidate diigits are #n, candidate diigits of this cell group are locked. Exclude candidate #n from other cells in the same House. Let's call this the N-th order LockedSet. When the diigit of cells/candidate is 5 or more, the remaining cell group of the same House is LockedSet. It is not necessary if you want to find the numeric array on the whole board. However, to pursue Sudoku's way of solving, is not it fun to find a big LockedSet? Later, i will show them.
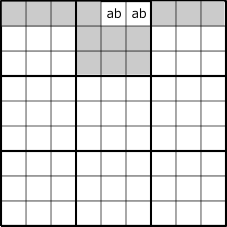
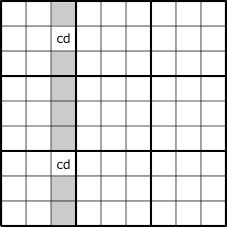
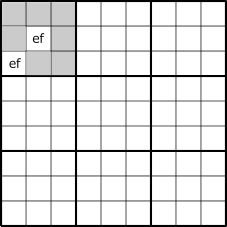
The following figure is an image of "LockedSet" of "2 cell 2 diigit". When Locked to ab, cd, ef, these candidate can be excluded from candidate diigits of gray cells. When a human searches for LockedSet, the LockedSet between blocks (center in the figure below) is more difficult than it is in the same block, but in the case of a program it is almost unchanged.

The following figure shows an image of a cell group in which LockedSets of 3 cells 3 diigits(left) and 4 cells 4 diigits (right) are established. It means that the outer frame belongs to the same house (row, column, block). The figure above is a case where each cell contains the candidate diigit in the same way. Some candidate diigits may be missing as shown in the bottom row.

Hidden LockedSet

Naked LockedSet is a case where candidate diigits clearly appear in the cell. Hidden LockedSet is when there are other candidate digits in the cell and the group of diigits making up LockedSet is hidden.
In the following figure, the top three rows are extracted. Focusing on candidate diigit #26 is only in r1c13, and a Hidden LockedSet is established.
The definition of Hidden LockedSet is as follows.
For a house, when n candidate diigits are in only n cells, the diigit in this cell is locked. Therefore, non-target candidate diigits in the same cell group are excluded.

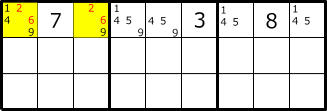
The following figure is an example of LockedSet.
The left figure is 2-LockedSet(Naked), r6c45(block b5) are candidate diigits #38.
The right figure is 2-LockedSet(Hidden). Focusing on c8, the diigit #16 enters only 2 cells of r19c8. Therefore, in this two cells the remaining diigit #349 can be excluded from the candidate.

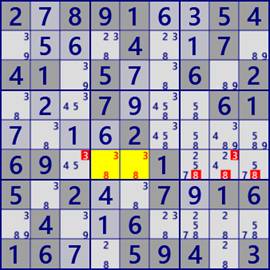
2.891..54....4..7.41.5..6.2...7...61....2....69...1...5.2..7.16.4..6....16..594.3
...857.....736.2...6...48..142..86..57......26.35..47..216.3........1.......2....

The following left figure is an example of 3-LockedSet(Hidden). For r4c23 and r5c2 of block b4, 3-LockedSet of 3 cells and 3 diigits is established for candidate diigit #249. The figure on the right is an example of 4-LockedSet (Naked). Focusing on r3789c9, 4-Locked Set of 4 cells 4 diigits is established for the diigit #3459. Also, 4 rows 4 digits 4-LockedSet(Hidden) is established for r1456c9#1678. It is a LockedSet paired with a yellow cell group.

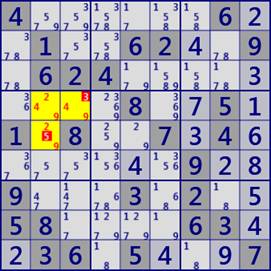
4......6..1..62..9.624.........8..5.1.8..7.4.......9..9...3.2..58....63..36.5...7
.8.........4..71.2.6718.39..2..3.9....38.52....5.1..3..18.4.67.4.96..8.........1.

Please think a moment here before proceeding.
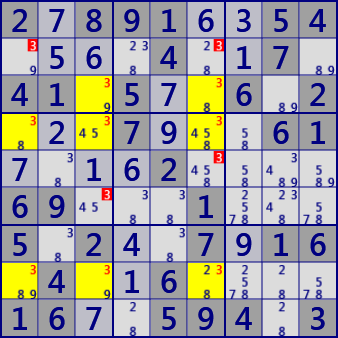
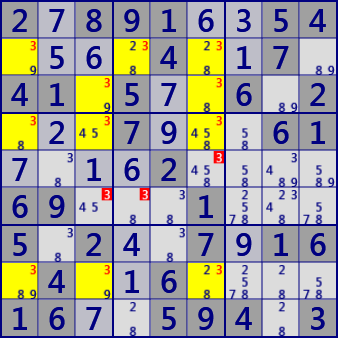
The first example of this page (2789 ... from the top left) shows LockedPair(2-LockedSet) of r6c45#38, There are other LockedSets. Please try looking.

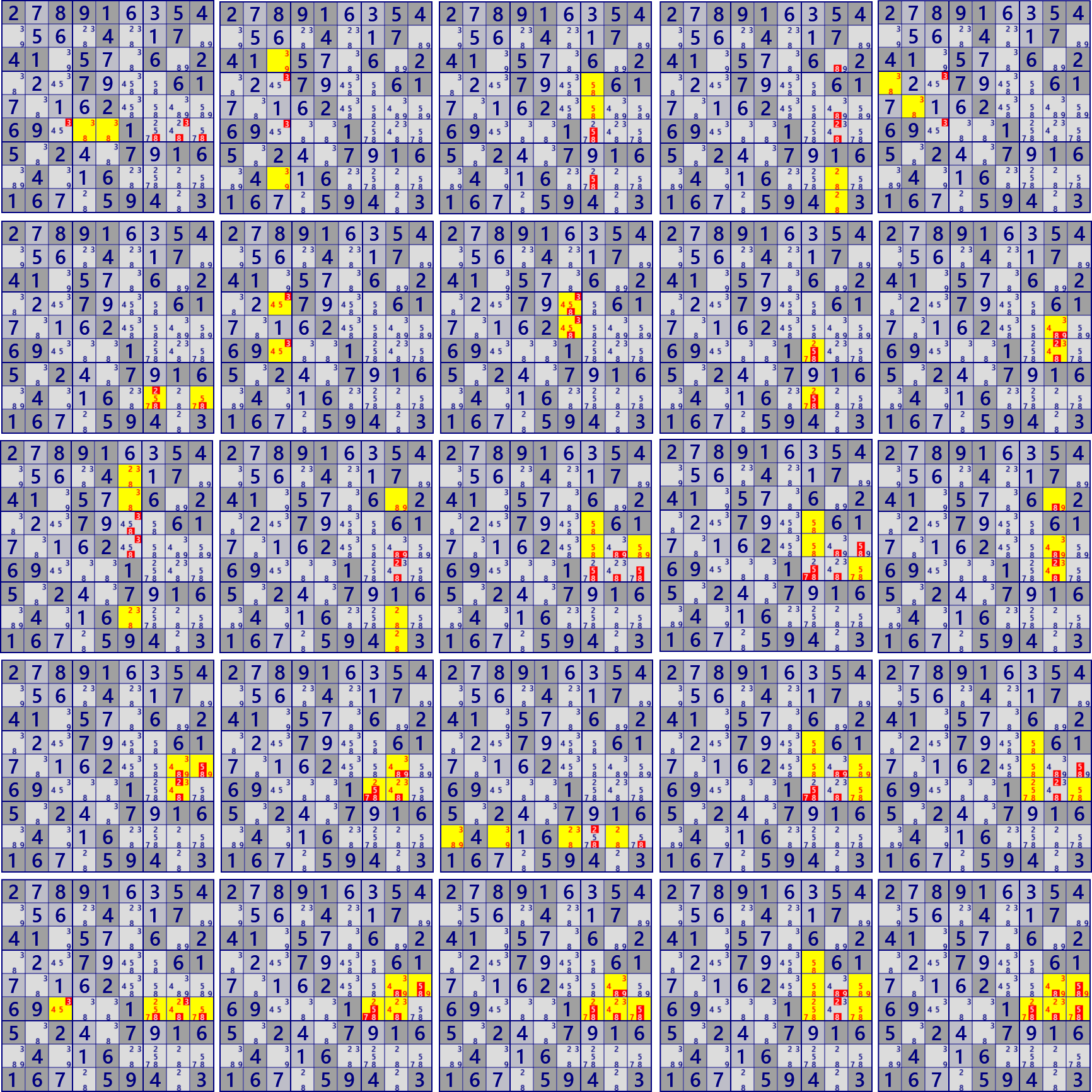
There are 25 LockedSets in this scene of this problem. We also find complementary LockedSets.

1. Locked Pair[2D] r6c45 #38
2. Locked Pair[2D] r38c3 #39
3. Locked Pair[2D] r45c7 #58
4. Locked Pair[2D] r89c8 #28
5. Locked Pair[2D] r4c1 r5c2 #38
6. Locked Pair[2D] (hidden) r8c79 #57
7. Locked Pair[2D] (hidden) r46c3 #45
8. Locked Pair[2D] (hidden) r45c6 #45
9. Locked Pair[2D] (hidden) r68c7 #27
10. Locked Pair[2D] (hidden) r56c8 #34
11. Locked Triple[3D] r238c6 #238
12. Locked Triple[3D] r389c8 #289
13. Locked Triple[3D] r4c7 r5c79 #589
14. Locked Triple[3D] r45c7 r6c9 #578
15. Locked Triple[3D] (hidden) r356c8 #349
16. Locked Triple[3D] (hidden) r5c89 r6c8 #349
17. Locked Triple[3D] (hidden) r5c8 r6c78 #234
18. Locked Quartet[4D] r8c1368 #2389
19. Locked Quartet[4D] r4c7 r5c79 r6c9 #5789
20. Locked Quartet[4D] r4c7 r5c7 r6c79 #2578
21. Locked Quartet[4D] (hidden) r6c3789 #2457
22. Locked Quartet[4D] (hidden) r5c89 r6c78 #2349
23. Locked Quartet[4D] (hidden) r5c8 r6c789 #2347
24. Locked Set[5D] r4c7 r5c79 r6c79 #25789
25. Locked Set[5D] (hidden) r5c89 r6c789 #23479

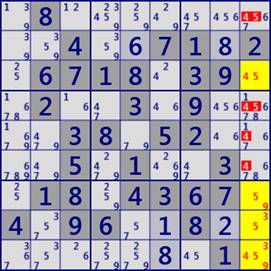
In addition, there is Fish to explain on another page.

1. SwordFish #3 BaseSet:R348 CoverSet:C136
2. JellyFish #3 BaseSet:R2348CoverSet:C1346

Thus, there are several steps to solve Sudoku. The method is different, but the cells/digits to be confirmed or excluded may be the same.

Fish(left:SwordFish right:JellyFish）

LockedSet program

LockedSet is a method of excluding candidate digits of cells in House. The analysis program is shown below.
This parsing routine leaves most of the details to subcontracted functions.
The sub-function has two arguments, degree and naked/hidden, and solves a naked LockedSet when the second argument is false. Solves hidden when true. The sub-function qualifies and excludes candidate digits in the following steps.

public class LockedSetGen: AnalyzerBaseV2{
    public LockedSetGen( GNPX_AnalyzerMan AnMan ): base(AnMan){ }

    public override void Initialize(){ /*Console.WriteLine("LockedSetGen");*/ }

    public bool LockedSet2(){ return LockedSetSub(2,false); }
    public bool LockedSet3(){ return LockedSetSub(3,false); }
    public bool LockedSet4(){ return LockedSetSub(4,false); }
    public bool LockedSet5(){ return LockedSetSub(5,false); }
    public bool LockedSet6(){ return LockedSetSub(6,false); }
    public bool LockedSet7(){ return LockedSetSub(7,false); }
    
    public bool LockedSet2Hidden(){ return LockedSetSub(2,true); } 
    public bool LockedSet3Hidden(){ return LockedSetSub(3,true); }
    public bool LockedSet4Hidden(){ return LockedSetSub(4,true); }
    public bool LockedSet5Hidden(){ return LockedSetSub(5,true); } 
    public bool LockedSet6Hidden(){ return LockedSetSub(6,true); }
    public bool LockedSet7Hidden(){ return LockedSetSub(7,true); }

    public bool LockedSetSub( int sz, bool HiddenFlag ){
        string resST="";
        for( int tfx=0; tfx<27; tfx++ ){
            List<UCell> BDLstF = pBDL.IEGetCellInHouse(tfx,0x1FF).ToList();
            int ncF = BDLstF.Count;
            if( ncF<=sz ) continue;
            
            Combination cmbG = new Combination(ncF,sz);
            while( cmbG.Successor() ){
                BDLstF.ForEach(p=>p.Selected=false);
                Array.ForEach(cmbG.Cmb, p=> BDLstF[p].Selected=true );

                int noBSel=0, noBNon=0;
                BDLstF.ForEach(p=>{
                    if( p.Selected ) noBSel |= p.FreeB;
                    else             noBNon |= p.FreeB;
                } );                  
                if( (noBSel&noBNon)==0 ) continue;

                //===== Naked Locked Set =====
                if( !HiddenFlag ){
		            .
		            . (Solution report code)
		            .
					return true;
                }

                //===== Hidden Locked Set =====
                if( HiddenFlag ){
                    if( noBNon.BitCount()==(ncF-sz) ){
		            .
		            . (Solution report code)
		            .
					return true;
                    }
                }
            }
        }
        return false;
    }
}