Sudoku Algorithm 4

General Logic

General Logic is a method common to most Sudoku solving algorithms. General Logic is a generalization of BaseSet/CoverSet. You need to understand the Fish algorithm. The first step of the Fish extension is (Finned) Franken/Mutant Fish.
This section is based on
A General Logic for Sudoku(www.sudokuone.com/sweb/general.htm).

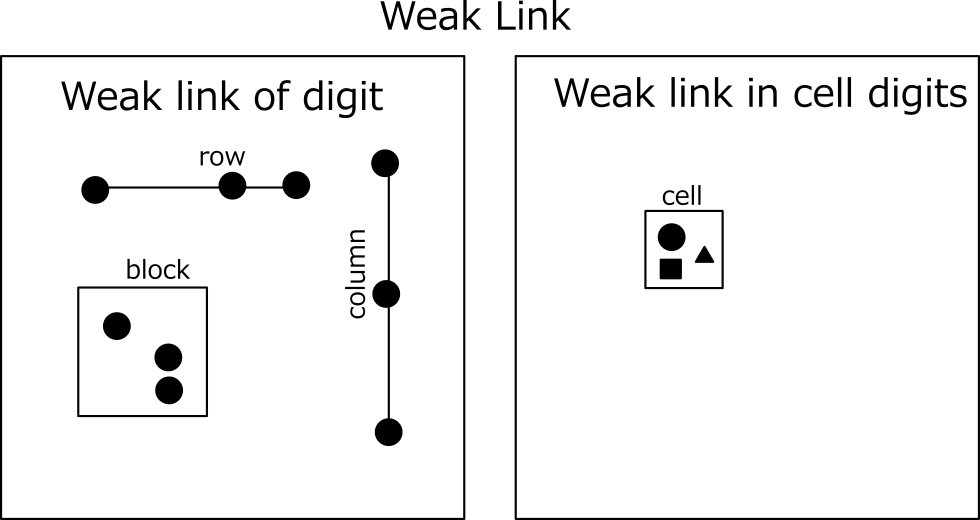
Weak link

GeneralLogic's basics are weak link.
Sudoku has constraints on rows, columns and blocks. Franken/Mutant Fish is a solution algorithm composed of rows, columns, and blocks.  Furthermore, from the Sudoku rule that any digit from 1 to 9 enters for 9x9 cells, each cell is also weak link. In total, Sudoku has 324 constraints.
general Logic is a solution algorithm composed of weak links in rows, columns, blocks, and cells. (Strong links are included in weak links.)

General Logic

BaseSet, CoverSet, Rank

BaseSet : Select n weak links so that they do not overlap. This n weak links are called BaseSet(n-BaseSet). There is one truth for each weak link, and there are n truths for BaseSet as a whole.

CoverSet : Choose m(m≧n) weak links different from BaseSet to completely cover BaseSet. This is called CoverSet(m-CoverSet). Elements that do not belong to BaseSet are acceptable. In order for General Logic to be established, elements that do not belong to BaseSet are necessary. CoverSet may overlap.The true number of CoverSet is m or less.

Rank : Define the ranking of BaseSet and CoverSet pairs as follows.
BaseSet/CoverSet Rank=m-n

General Logic

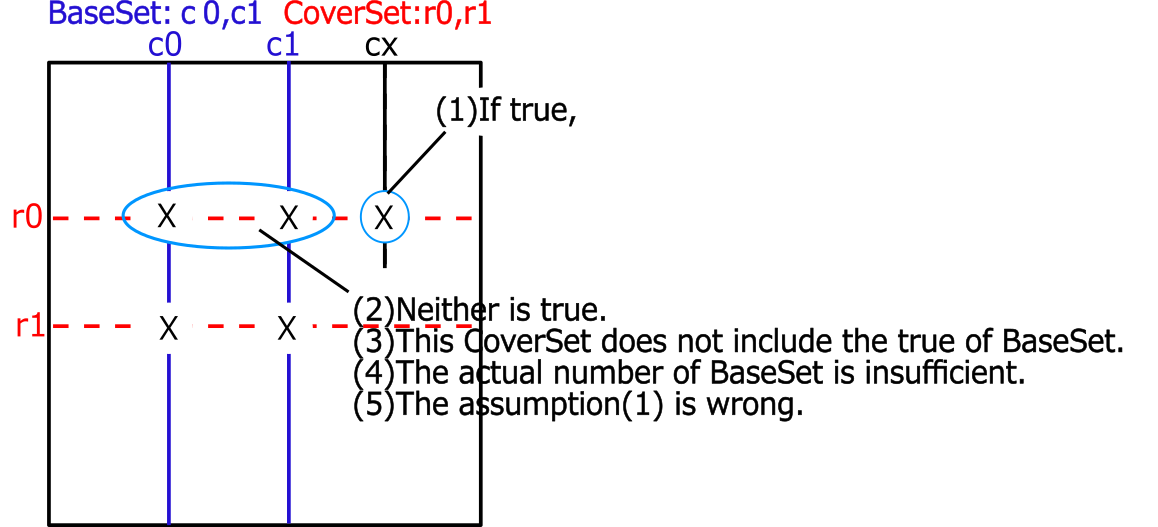
rank 0:

When the n-CoverSet completely covers the n-BaseSet, the cells/digits of CoverSet-BaseSet (difference set) are not true. If the difference set is empty, the logic here does not hold.
If true, the weak link containing it will have no truth in the intersection with BaseSet. Therefore, n-1 true is included in CoverSet∩BaseSet. In other words, BaseSet got lost. Therefore, the first assumption is incorrect.
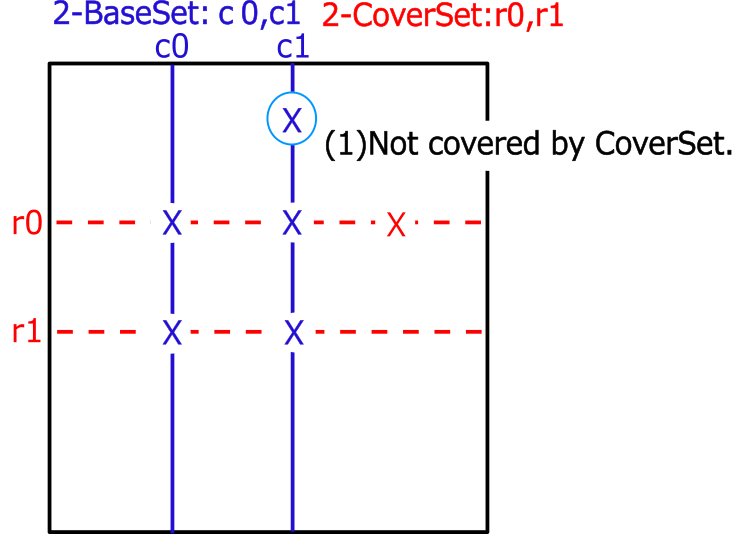
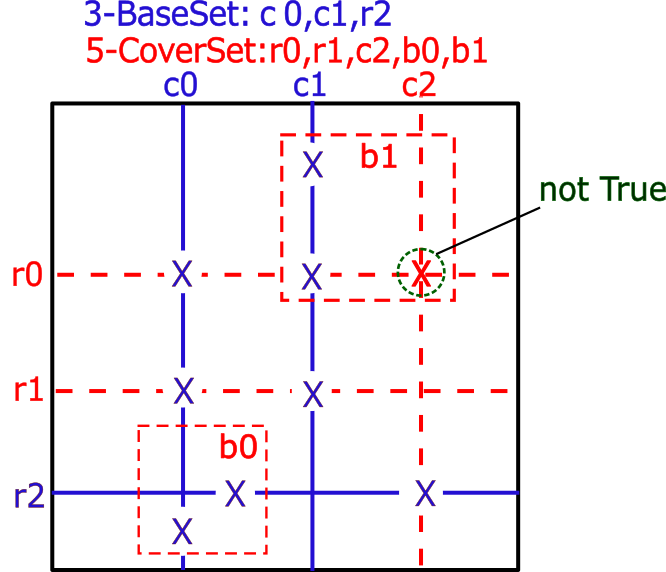
The following figure is the simplest Fish BaseSet(column) and CoverSet(line). Check BaseSet and CoverSet, BaseSet-CoverSet(difference), BaseSet∩CoverSet(common) . Note that BaseSet-CoverSet is not limited to one element. Even if there are two or more, all of them can be excluded.

General Logic

rank 1:

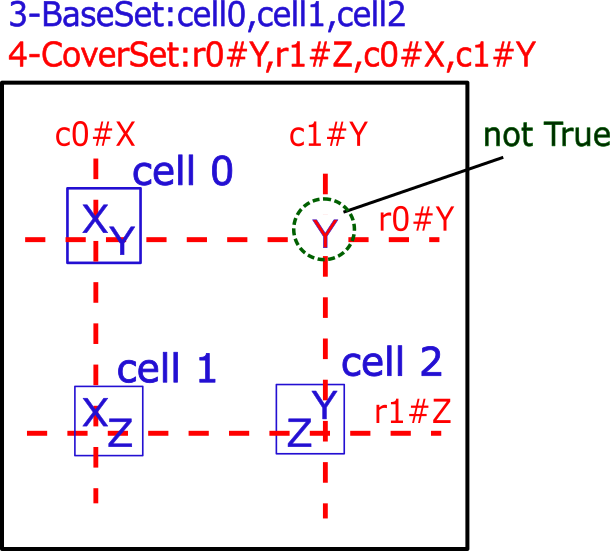
Consider the case of covering n-BaseSet with (n+1)-CoverSet.
The choice of CoverSet covering n-BaseSet is free. In order to be an analysis algorithm, the following conditions must be satisfied.
Condition 1:(n+1)-CoverSet completely covers n-BaseSet.
Condition 2:Two of the (n+1)weak links of CoverSet have elements in common which are not included in the n-BaseSet.
When these conditions are satisfied, the elements of the intersection of condition 2 are not true.
Assumed that the digit X of the common part is true. Since digit X is not included in Baseset and is contained in two weak links of CoverSet, there are n-1 weak links of CoverSet including true of BaseSet. The first assumption is incorrect as the true digit of BaseSet is insufficient.





Next is an example of rank 1, BaseSet are 3 cells, CoverSet are 4 rows/columns.

General Logic

rank k(k≧1):

Consider the case of covering n-BaseSet with (n+k)-CoverSet.
The configuration is the same as Rank 1. In order to be an analysis algorithm, the following conditions must be satisfied.

When these conditions are satisfied, the elements of the intersection of condition 2 are not true.
Assumed that the digit X of the common part is true. Since digit X is not included in Baseset and is contained in (k+1) weak links of CoverSet, there are n-1 weak links of CoverSet including true of BaseSet. The first assumption is incorrect as the true number of BaseSet is insufficient.


General Logic

General Logic program code

General Logic program code is in GNPX proj Sudoku analysis application source project . The algorithm is relatively simple, since Fish is extended to rows, columns, blocks, and cells. However, be aware of the following points.

General Logic is logic to exclude cells/digits that break Locked as "not true". There is no way to decide which cell/digit the candidate is unique. In addition to General Logic, you need code to fix (eg Single).

Minimum programs to solve Sudoku can be configured with "single+General Logic".
However, GeneralLogic's search has a larger computational complexity than the conventional method, which is a major practical problem. In the current version of GNPX, it took several tens of minutes to solve the 4th order GeneralLogic (using some speed-up procedures). It can not be solved within the practical use time for the 5th or higher order or the rank 2 or more.
Original paper is A General Logic for Sudoku, there is an sample of 7th rank 3.

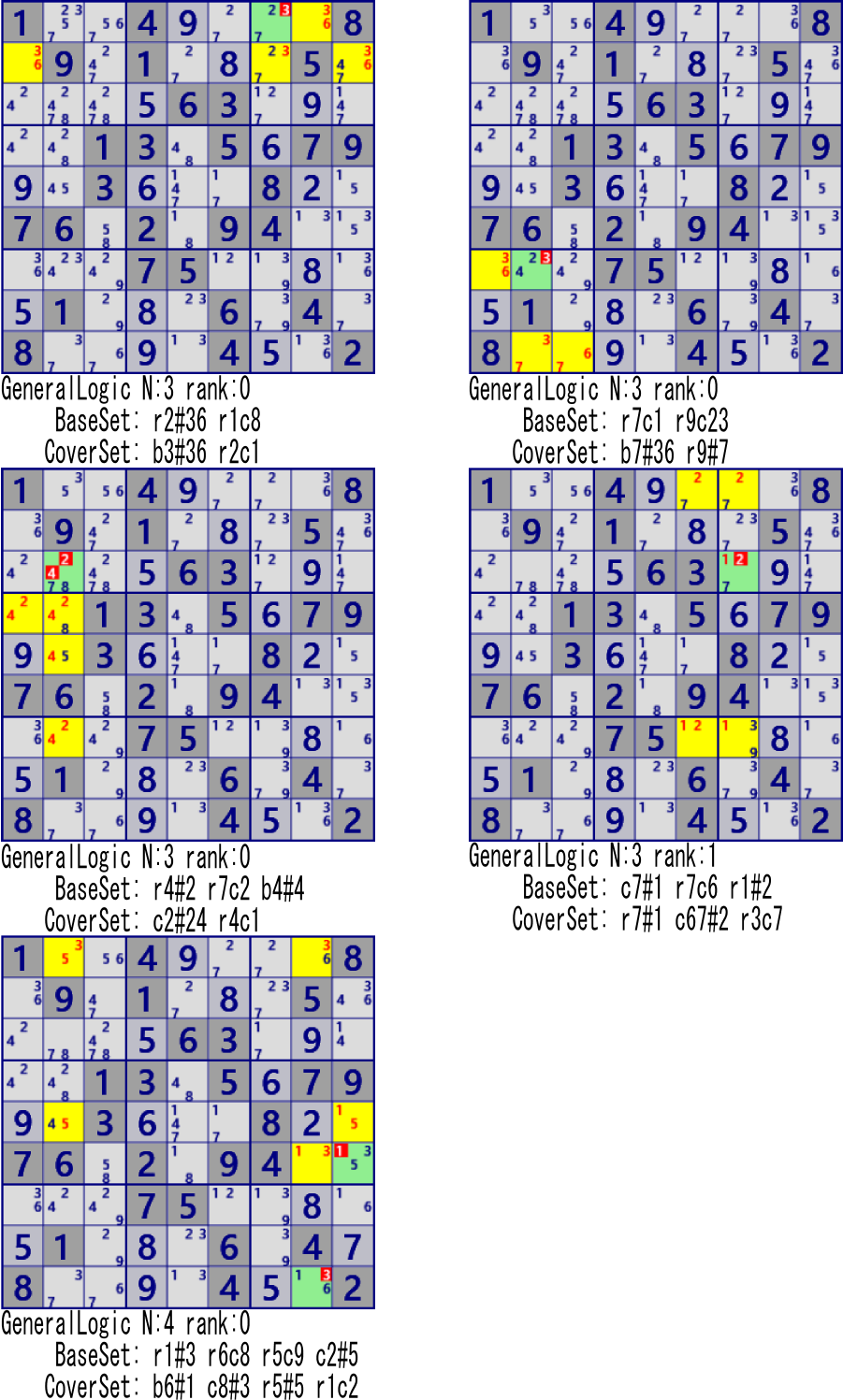
Sample of General Logic solution

Here is an sample of GeneralLogic solution. In the upper, cells and digits excluded as "LockedTriple [3D] r459c2#168 r37c2#1 is not True" are the same, but there is no solution corresponding to the conventional method.
The lower can exclude the same cell/digit in ALS-XZ(Singly Linked) (lower right). However, the method used is quite different.

General Logic

3..5....2.5.2...1.....36.....59.7.31..9...4..23.8.46.....79.....7...8.4.8....2..9
5..7....3.3.4...6.....36.....45.1.29..9...4..68.9.27.....27.....1...3.5.7....5..4

As shown in the following table (application sample of General Logic), the solution of the conventional method can be reinterpreted by GeneralLogic.
The next sample is the 4th order General Logic (rank 0,1). In this way, the conventional method may not correspond to the GeneralLogic solution. GeneralLogic shows that it is a more general solution.
General Logic

1..4....8.9.1...5.....63.....13.5.79..3...8..76.2.94.....75.....1...6.4.8....4..2

It is also an issue to explore the new solution from the GeneralLogic solution.

Application sample of General Logic

An sample of applying General Logic to scenes solved by a normal Sudoku algorithm is shown.
"Single" is definite of the cell/digit where the candidate became unique, so GeneralLogic is not necessary, it is shown as the smallest application sample of BaseSet/CoverSet.

Algorithm Sample BaseSet CoverSet Comment
Single/
LastDigit

BaseSet:b1#6

Coverset:c3#6		 rank0
r68c3#6 is not true
Single/
Naked

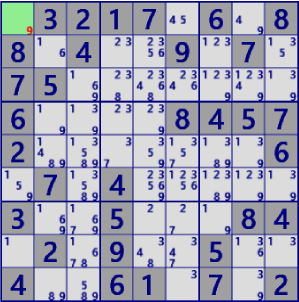
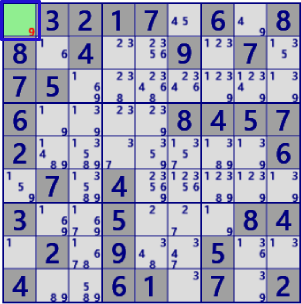
BaseSet:r1c1

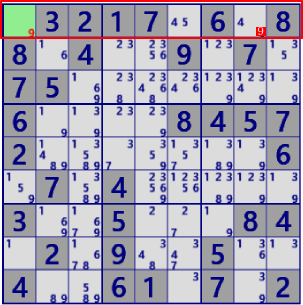
Coverset:r1		 rank0
r1c8#9 is not true
Single/
Hidden Single

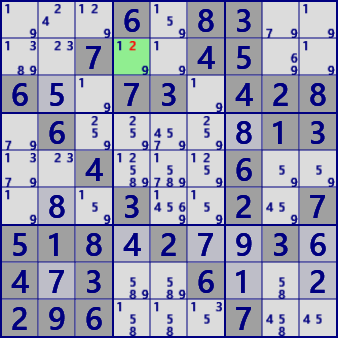
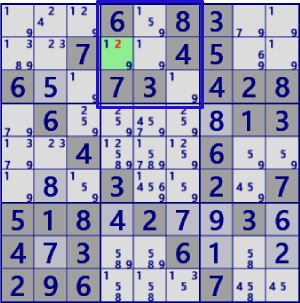
BaseSet:b2#2

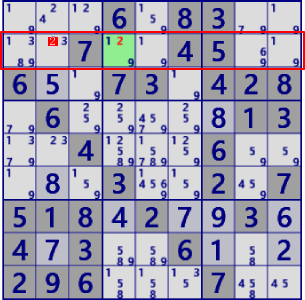
Coverset:r2#2		 rank0
r2c2#2 is not true
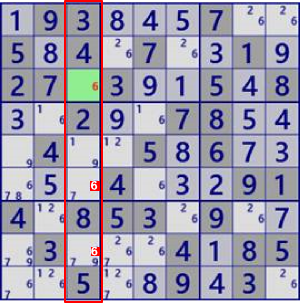
LockedCandidate/
(type1)

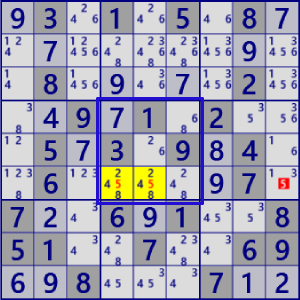
BaseSet:b5#5

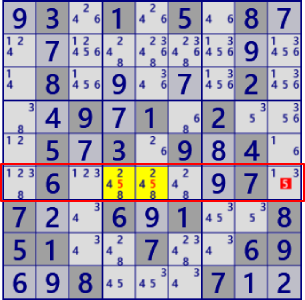
Coverset:r5#5		 rank0
r5c9#5 is not true
LockedCandidate/
(type2)

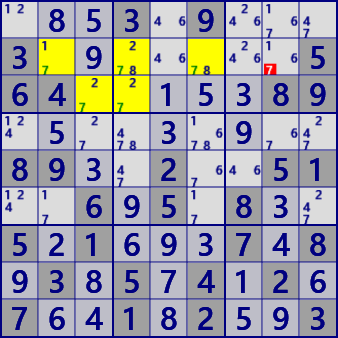
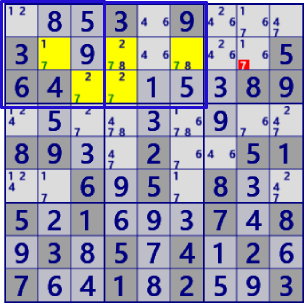
BaseSet:b12#7

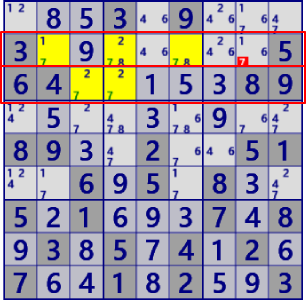
Coverset:r23#7		 rank0
r2c8#7 is not true
LockedSet/Naked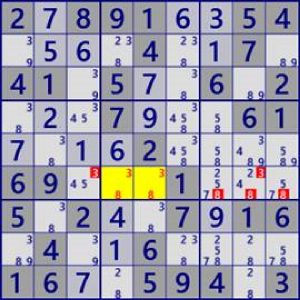

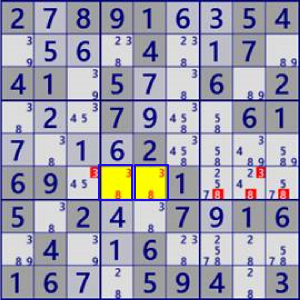
BaseSet:r6c45

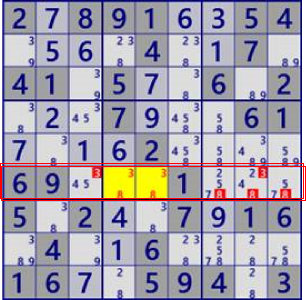
Coverset:r6#38		 rank0
r6c38#3 r6c789#8 is not true
LockedSet/Hidden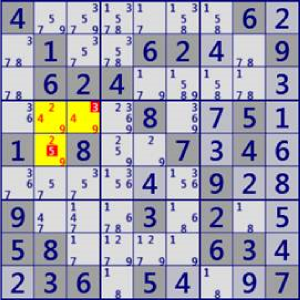

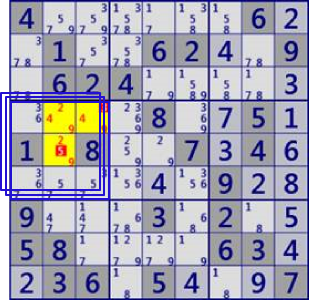
BaseSet:b4#249

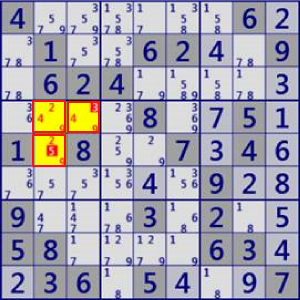
Coverset:
r4c23 r5c2 		rank0
r4c3#3 r5c2#5 is not true
Fish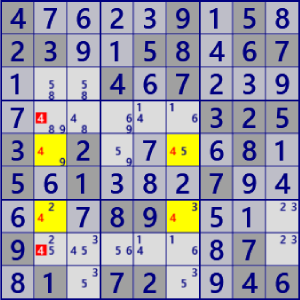

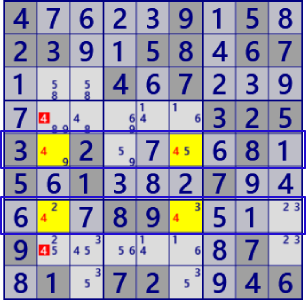
BaseSet:r57#4

Coverset:c25#4		 rank0
r48c2#6 is not true
FinnedFish

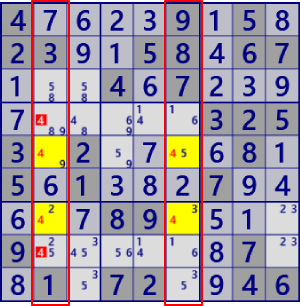
BaseSet:r17#4

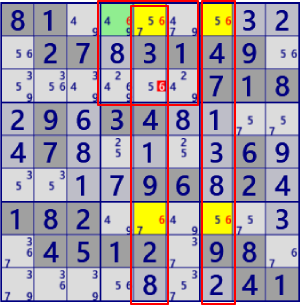
Coverset:
c57#4 b2#4		 rank1
r3c5#4 is not true
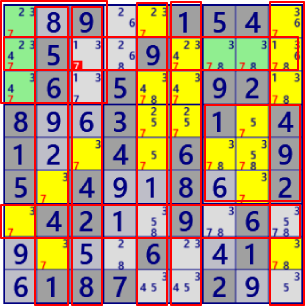
Franken/Mutant Fish

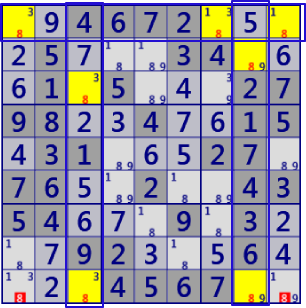
BaseSet:
r1#8 c38#8

Coverset:
r9#8 b13#8		 rank1
r9c19#8 is not true
Finned F/M Fish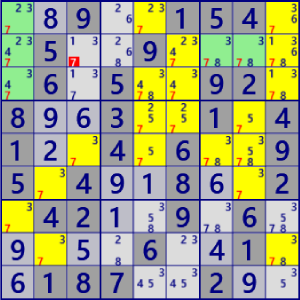

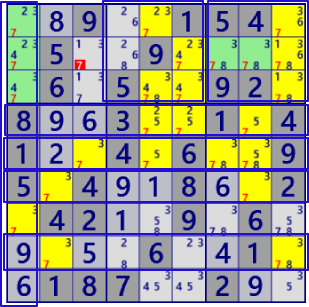
BaseSet:
r4568#7 c1#7 b23#7

Coverset:
r27#7 c23569#7 b16#7		 rank2
r2c3#7 is not true
SkyScraper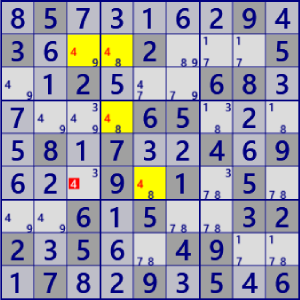

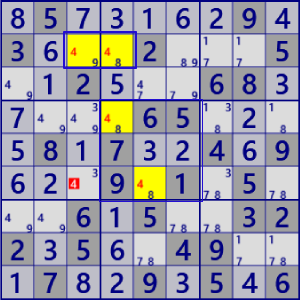
BaseSet:
r2#4 b#4

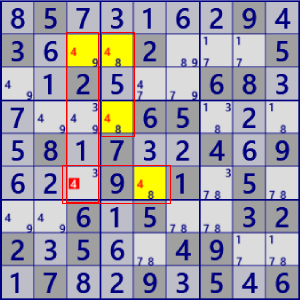
Coverset:
C34#4 r6#4		 rank1
r6c3#4 is not true
EmptyRectangle

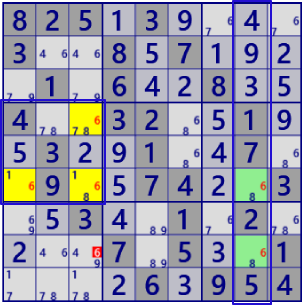
BaseSet:
c8#6 b4#6

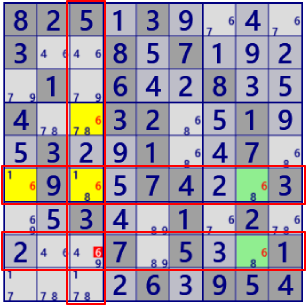
Coverset:
r68#6 c3#6		 rank1
r8c3#6 is not true
X-Chain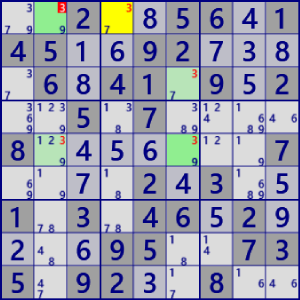

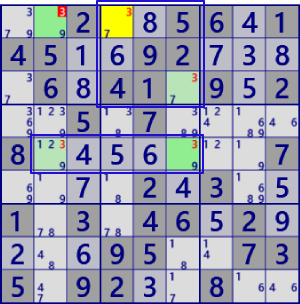
BaseSet:
r5#3 b2#3

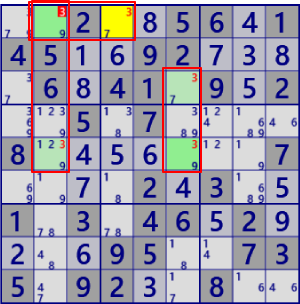
Coverset:
r1#3 c25#3		 rank1
r1c2#2 is not true
XY-Chain

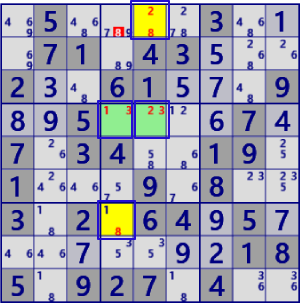
BaseSet:
r1c5 r4c45 r7c4

Coverset:
r1#8 c2#2 r4#3 c4#1 c4#8		 rank1
r1c4#8 is not true
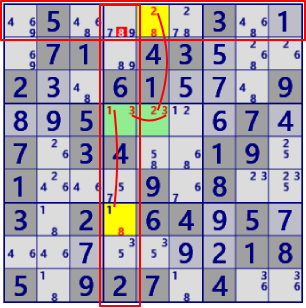
ColoringTrap

BaseSet
:r1#5 C49#5

Coverset:
b239#5 C7#5		 rank1
r7c8#5 is not true
ColoringWrap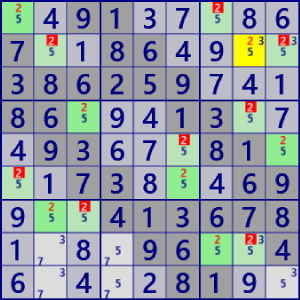

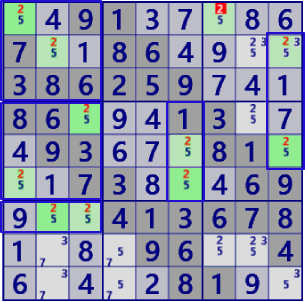
BaseSet:
r7#5 C69#5 b14#5

Coverset:
r156#5 C23#5 b3#5		 (左図例はBase/CoverSetによる解が重なっている。）

rank1
r1c7#5 is not true
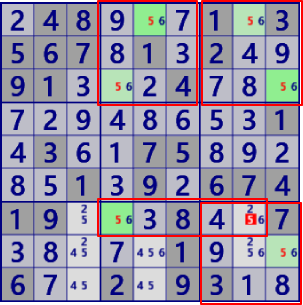
MultiColoringType1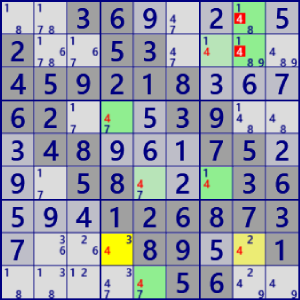

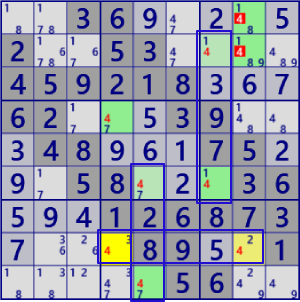
BaseSet:
r8#4 c58#4

Coverset:
r5#4 C8#4 b33#4		 rank1
r12c8#4 is not true
MultiColoringType2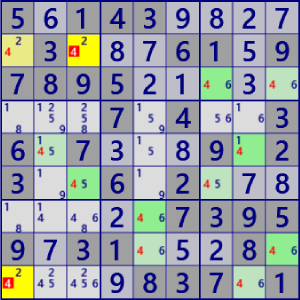

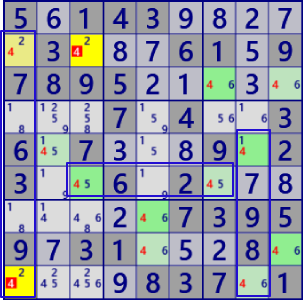
BaseSet:
r6#4 c18#4

(BaseSetに含む
セルのみが対象)

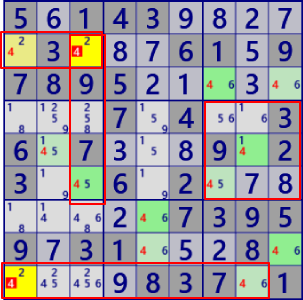
Coverset:
r29#4 c3#4 b6#4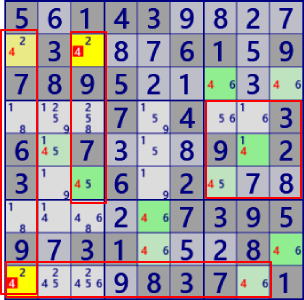
 


Coverset:
r9#4 c12#4 b6#4
rank1
r2c3#4 is not true







rank1
r1c9#4 is not true
XY-Wing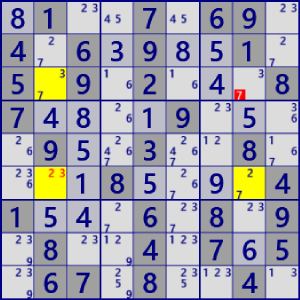

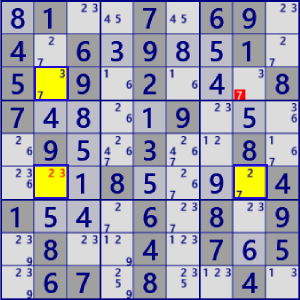
BaseSet:
r36c2 r6c8

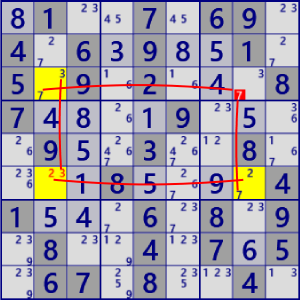
Coverset:
r3#7 r6#2 c2#3 c8#7		 rank1
r3c8#7 is not true
W-Wing

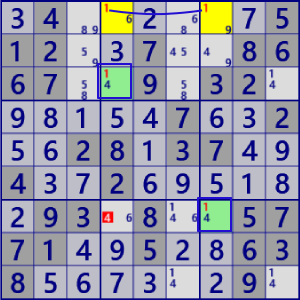
BaseSet:
r3c4 r7c7 r1#1

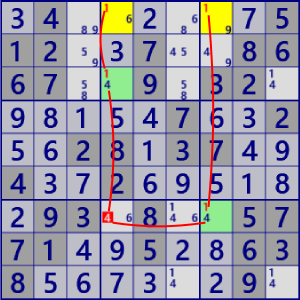
Coverset:
r7#4 c4#14 c7#1
 rank1
r7c4#4 is not true
RemotePair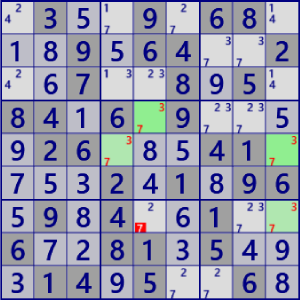

BaseSet:
r4c5 r5c4 r5c9 r7c9

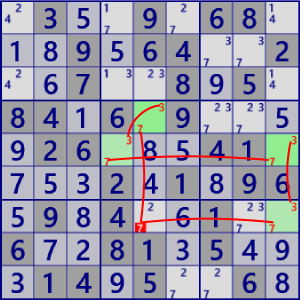
Coverset:
r57#7 c5#7 c9#3 b5#3		 rank1
r7c5#7 is not true
XYZ Wing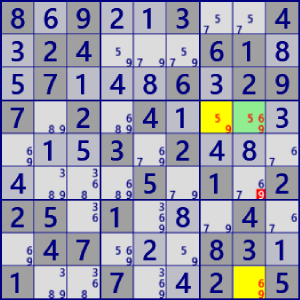

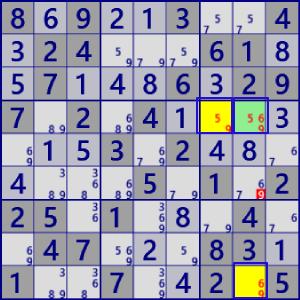
BaseSet:
r4c78 r9c8

Coverset:
r4#5 c8#69 b6#9		 rank1
r6c8#9 is not true
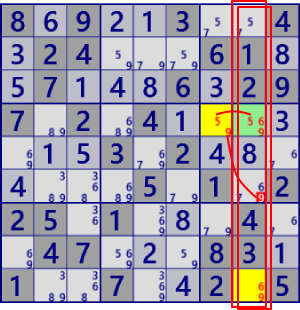
XYZ Wing(ALS)

BaseSet:
r36c1 r456c2

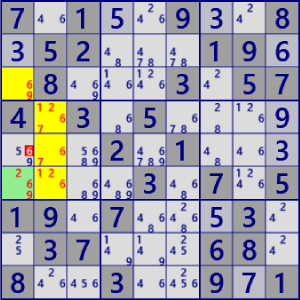
Coverset:
c1#69 b4#1267
(表示略） 		rank1
r5c1#6 is not true
SueDeCoq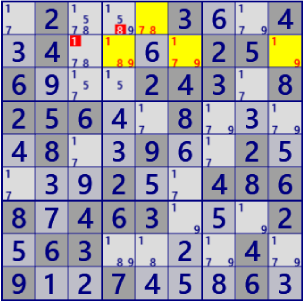

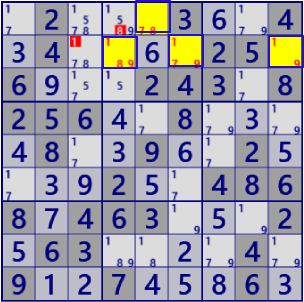
BaseSet:
r1c5 r2c469

Coverset:
c2#19 b2#78		 rank0
r2c3#1 is not true
ALS XZ(SinglyLinked)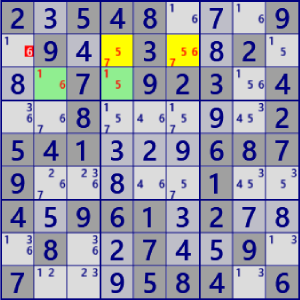

BaseSet:
r2c46 r3c24

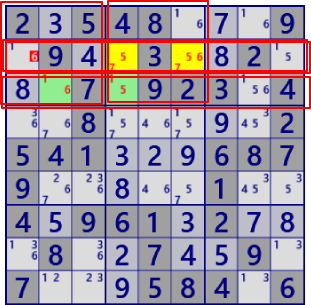
Coverset:
r2#67 r3#1 b1#6 b2#5		 rank1
r1c2#6 is not true
ALS XZ(DoublyLinked)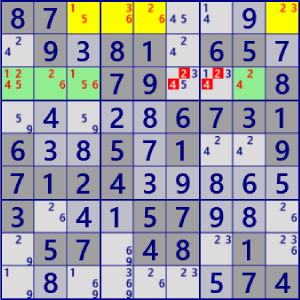

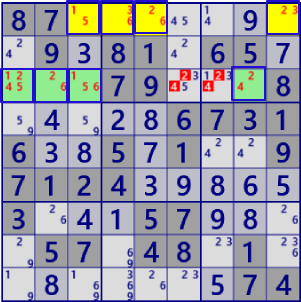
BaseSet:
r1c3459 r3c1238

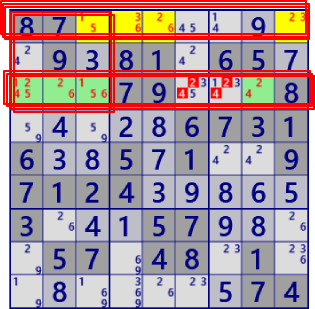
Coverset:
r1#236 b3#24 b1#156		 rank0
r2c67#24 is not true
ALS XY-Wing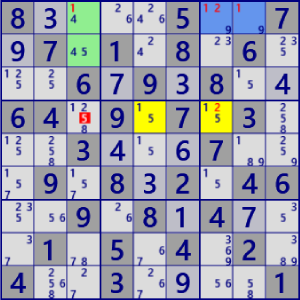

BaseSet:
r1c78 r12c3 r4c57

Coverset:
r14#1 r1#9 c3#45 c7#2 		rank1
r4c3#5 is not true
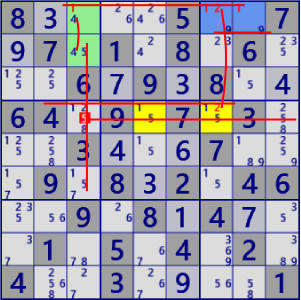
ALS Chain

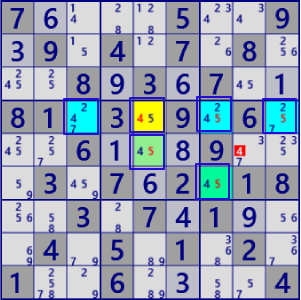
BaseSet:
r4c5 r4c379 r5c5 r6c7

Coverset:
r4#247 r5#4 c6#4 b6#45		 rank1
r5c8#4 is not true
ALS DeathBlossom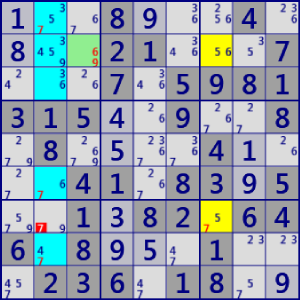

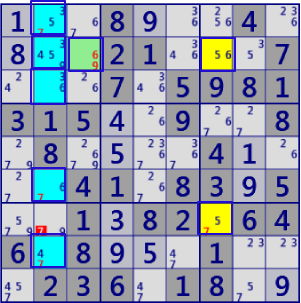
BaseSet:
r2c3 r12368c2 r27c7

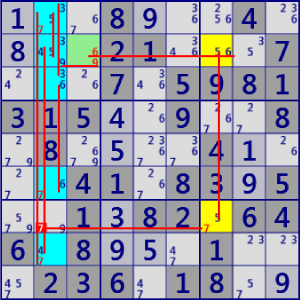
Coverset:
r2#69 r7#7 c2#34567 c7#5		 rank1
r7c2#7 is not true
NiceLoop Continuous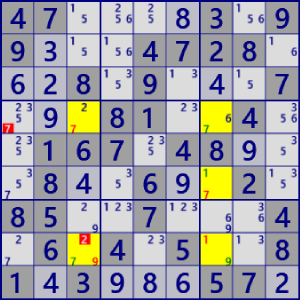

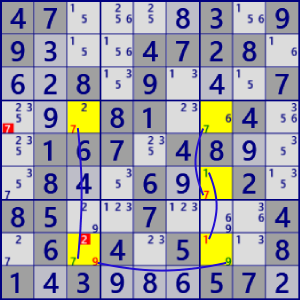
BaseSet:
r8#9 c36#7 c6#1

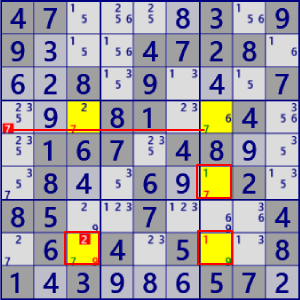
Coverset:
r4#7 r6c7 r8c37		 rank0
r4c1#7 is not true
NiceLoop Discontinuous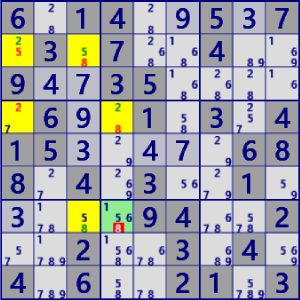

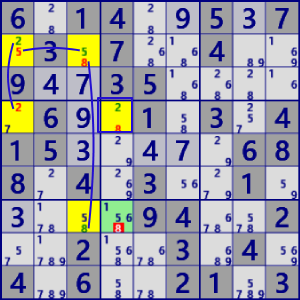
BaseSet:
r2#5 c1#2 c3#8 r4c4

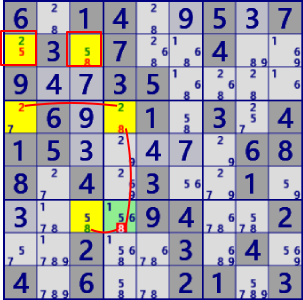
Coverset:r2c13 r4#2 r7#8 c4#8		 rank1
r7c4#8 is not true